フーコーの振り子が緯度ごとに回転角が変わるしくみ（と計算機）

9月18日は物理学者フーコーさんの誕生日(1819/09/18 – 1868/02/11)です。フーコーと言えば振り子実験が有名ですよね～。

…っていうさらっとした話を書くつもりだったのですが、それだけではアレなのでフーコー振り子の仕組みをまったり味わう緯度別 回転角 計算機もつけました。

フーコーの振り子とは…

フーコーの振り子とは、振り子によって地球の自転を可視化した装置です。…って書いても良く判らんけど、ものとしてはただの長い振り子です。

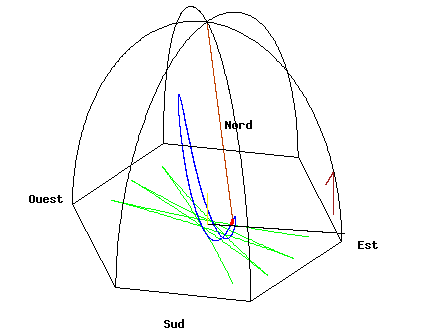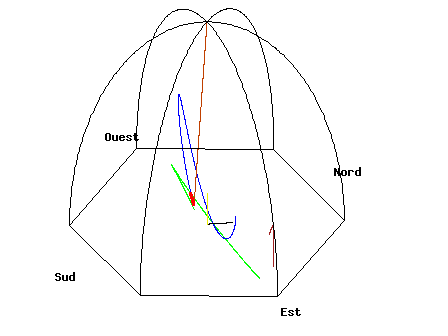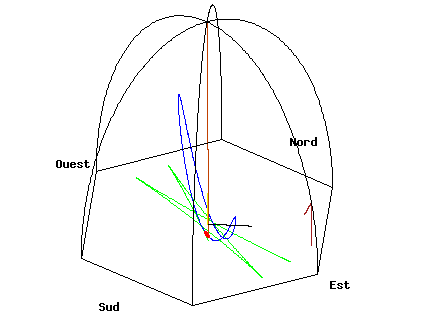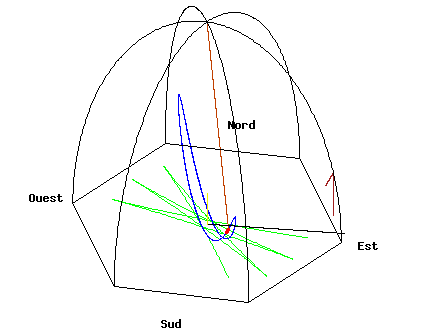
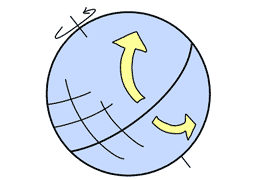
地上で観察していると「振り子に対して回転力が働いてるように見えます」が、実は宇宙から見ると振り子は単純な往復運動をしてるだけなのがミソ。勝手に回転してるのは地球と観測者です。いずれにせよ、その相対によって地球の自転が観測出来るという仕組みです。

このときの回転力はコリオリの力と呼ばれていて、振り子を設置した緯度によって向きと強さが少しずつ変わります。赤道ではほとんど動きませんが、極だと1日でぐるっと一周します。

あと、フーコーがこの現象を明らかにしたときに『「こんな実験は既に誰かがやってるだろう」って調べたけど先行文献は見つからなかった』って話が結構好き。

フーコー振り子 緯度ごと回転角 計算機

動きが緯度ごとに違うと言ってもどれくらい動くのか判りにくいので、ざっくりデモ作りました。

観察地点の緯度	度(deg)
観測時間	時間
回転移動した角

フーコー振り子 回転角計算機　パラメータ詳説

項目	有効な数字	詳細
観察地点の緯度	0 ～ ±90	単位：度(deg) プラスは北半球・マイナスは南半球 0は赤道 ±90は極 初期値は東京（上野）
観　測　時　間	0 ～ 24	単位：時間 1日が24、30分は0.5、6分が0.1 （無意味だけど）マイナスは過去に相当
回転移動した角		単位：度(deg) 180で半周・360で一周 プラスは時計回り・マイナスは反時計回り

思いつきで作ったのでインターフェイス適当です～。初期状態で「計算する」ボタンを押すと上野で11時間フーコーの振り子を観察した回転角が表示されます。緯度や観測時間を書き換えて色々試してみて下さい。

フーコー振り子 計算機の遊び方

まず試して欲しいのが赤道(緯度0)と北極・南極（±90）です。

時間を変えるとどんな値になるでしょう?　特に極で色々いじるとフーコー振り子のイメージが掴めます。

あとはお住まいの地域で適当な値に入力してみて下さい。

フーコー振り子　見どころ

各地の設置状況を見てみたら、結構色んな場所にあるんですね。科学館に次いで展示されてるのは大学よりも高校の方が多くて驚きました。でもそれってすごく良い話。(^^

フーコー振り子の主な鑑賞ポイントは、次のような点に注目すると面白いんじゃないかと思います。

• ワイヤー長さと振り子周期など展示物のスケールを鑑賞する
• 盤面のデザインを楽しむ
• 地面に刻まれた目盛り間隔から数時間後の位置を想像してまったりする
• ワイヤーの太さや接合部を見て空気抵抗に対する工夫を評価する
• 吊ってる支点の構造を見て摩擦に対する工夫を評価する

中性的なモチーフだったり質実剛健だったり、それぞれの違いが見えてきて意外と面白いです。

国立科学博物館のフーコー振り子

鑑賞例として科博のフーコー振り子を取り上げてみます。常設館の地下一階に、4階から吊った大きな振り子が展示されてますね。

日時計や方位磁針をイメージさせる定番のモチーフです。あと外周のLED照明は経過時が解りやすくて良いかも。

10分おきに青色灯が、正時になると赤色灯が、それぞれ点灯する仕組みです。もちろん、そのタイミングで振り子のおもりが目盛りの上を通過します。

最初このセンシングの仕組みがどうなってるのか気になって、色んな方向から覗いてみたんですけど　もしかしたらLEDは独立した時計で振り子と同期してないかも知んない。(^^;

ただ、仮に互いが連動してないとしても「位置合わせさえ正しければクォーツ時計と同等の工作精度が出る」という意味で素晴らしいね。

科博のフーコー振り子の回転角を計算する

ここで、上野におけるフーコー振り子の回転角を評価してみましょう。ちょっと潰れ気味だけど、冒頭の写真をよく覚えておいて下さい。

先ほど回転は設置緯度に依存すると書きましたが、振り子が1周するのに必要な時間は

1日 ÷ sinθ　で

さらに科博は（北緯）35.7度に位置しているので

1日 ÷ sin(35.7度）≒ 0.5835

これを来場者が開館中に観察できる（LEDが埋め込まれてる）時間帯の移動角に直すと

360度 ÷ (1日 / sin(35.7度)) × 11時間 ≒ 96.28度

となります。全部繋げるとこんな式。

360 / ( 24 / sin( 35.7deg ) ) * 11

このまま計算機なりGoogle検索に突っ込めば答えの値が出るので確認してみて下さいねん。