【本日πの日】クロッカスの花姿を数学的に検証してみる

3月14日はパイの日です。

お菓子じゃなくて、円周率のほう。

3月14日はΠの日＆アインシュタインとシェルピンスキーの誕生日

3月14日が、π（パイ：円周率）の日であると同時にアインシュタインの誕生日でもあることは非理系な方々にも食いついて貰えるちょっとした豆知識です。

でも個人的にはシェルピンスキーの誕生日であることを推したいキモチ。

相対性理論は言うに及ばず、位相幾何学なんかも大変意義深い分野として広く知られていながら「ざっくり判った気になってるだけ」の代表的な数理分野ですよね。

まぁ、とどのつまり自分も判ってない側なので深く掘り下げたつもりが墓穴にならないうちに さくっと切り上げます。

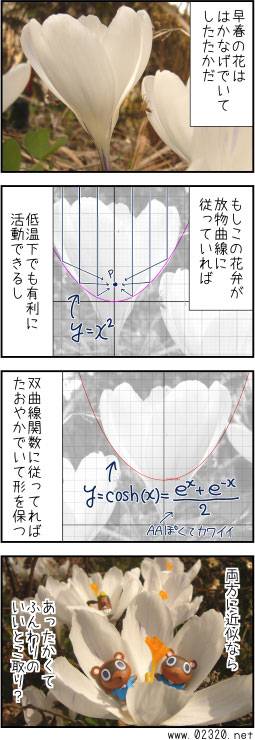
放物線と双曲線関数の間にある…クロッカス？

寒い寒いと言いつつも春は確実にやってくるのであって、気がつけば足下にクロッカスが咲いてるのを発見しました。

チューリップなんかもそうなんですけど、こういうコロコロした花って開花してからダメになるまでの間に開いたり閉じたりを繰り返すものが割と多いですよね。

おそらく風雨から雄しべや雌しべを守るためなんでしょうけど、花弁の開閉ってかなり体力を使う（=花期を縮める）ので本人(?)達にとっては決死の覚悟でやってる感が漂います。

寒さから身を守りたい　→　花弁が厚ければ暖かくなる
疲れる事はしたくない　→　花弁が薄ければ負荷は軽い

…の、両立を迫られているという前提で見ると　なかなか良く出来た花姿なんじゃないかと勝手に感心しております。

力を一点に集める性質があるパラボラ（＝放物線）

…というわけで寒いのがイヤだって話からパラボラの話。

Parabola ： y = x²

物を放り投げた軌跡を放物線といいますね。英語でパラボラと呼ぶとおり、テレビなどのパラボラアンテナはこの曲線から成り立ってます。

放物線、あるいはそれをy軸中心に回して得た放物面があったとき、正面から何かを当てると跳ね返される際に必ずある特定の一点を通るという性質があります。

つまり一点に何かを集めたいときパラボラは非常に便利。数学的な性質がそのまま機能として成立してて超うっとりしますね。

ちなみに、パラボラアンテナが製品ごとに曲率違うように見えても全て仲間です。焦点に対してどの曲面を切り取ってるかの違い。今後BSアンテナなどを見かけたら受信部の位置関係をそれぞれ見比べてみてください。

光を集めると暖かい

小学校の理科で鏡を使った集熱実験ってのがありますが、鏡面ほどの反射率がなくてもある程度の光を集めれば十分な加温効果があるんじゃないかと思います。

虫を呼んだり雄しべ・雌しべを寒さから守るのに都合が良さそうですね。

ともあれ、この特性を逆に用いると高指向性スポットライトも作れます。焦点Pに光源を置くと反射光がすべて軸方向に揃ってまっすぐ放出されるのです。

同様に、暮らしに根差した放物面としては中華鍋が有名。

この場合、裏から暖められた鉄板の熱は漫然と逃げることなく焦点Pへと向かいます。高温で仕上げたい中華料理で鍋を振るのはこのためですね。

製品の成り立ちとしては多分逆で、「弱い火力で効率よく調理するため放物面に近づいてった」のかな。フィードバックによる最適化が真理をとらえたと考えると胸熱です。

同じ理由から、平たいIH中華鍋を懸命に振り回してもあんまり意味ないです。IH自体の火力はガス同等かそれ以上ですから、鉄板焼きの要領で調理すると吉ですよん。

山田 鉄 打出片手中華鍋(板厚1.6mm) 24cm 以前( 2 ≦ x ≦ 4 )みたいな放物面である中華鍋を見たことがある気がするんですが、今はもう作られてないのかな。振るのが楽そうで一度試してみたかったんですが。

小さな部材でものを支えるのに適した　カテナリー

大きな板を下から支えるのは結構骨が折れるものですが、よく考えると花びらも下部一点で支えられてることに気づきます。

薄い花びらが自立してることも含めて力学的にみると割とすごいことなのでは。

Hyperbolic Cosine ： y = cosh(x) = (e^x + e^-x) / 2

ハイパボリックコサイン（双曲線関数）、グラフ引くと放物線と似てますが（4コマ参照）それぞれ微妙～に違います。

名前に双曲線とついてますが、

x² / a² – y² / b² = 1

…であるところの双曲線とも違います。

双曲線関数はどういう式かというと、ヒモとか自重がある長いものをだれ～んと垂らしたときに出来る曲線ですね。別名カテナリー ( Catenary / 懸垂線 ) とも言います。

重力に対して非常に安定的な形をしていますから、建築系の方にはお馴染みの関数かも。橋で用いられるケースが有名ですが、城・寺社の屋根もカテナリーに従ってることが多いです。サグラダファミリアの曲線もこれ。

重力に対して安定ということは、少ない材料で物を支える時に適した形といえるでしょう。

締め：巡り巡って話を戻す（Πの日なので）

二つのグラフに倣っているこの花の形状は　おそらく「少ない材料でめしべを守りたい」という問題を高いレベルでクリアしてます。

合理的な造形美というか、高度な生存戦略が見え隠れする感じ。能天気に「健気でカワイイ」とか言うの植物に失礼じゃないかと思ってます。

もっとも、「可憐な花を人の手で守ってやる」気でいたら「美しい花を見るために全力で世話をさせられている」だけってことはよくあるので、それはそれとして。

もともとは親指姫の話をするはずだったんですが

一応「全ての事象は必然だ！」みたいな流れにはなりましたが、もともと1枚目の写真に蜘蛛が映り込んでたところから親指姫の話をするつもりだったんですよね。

アンデルセンを普通に読み解いた上で親指姫の正体って実はハエじゃないのかな？…って話をするつもりだったんですが　かすりもしないまま軌道修正不可能な状況になってしまったので　このまま逃げ切りたいと思います！

【0131】 ダンボール製太陽光調理器 エコ ソーラークッカー 1個

とびだせ どうぶつの森　【楽天】 / 【Amazon】 フィギュアにまめつぶ使いました。よく考えたらピクミンフィギュアのほうが1/1スケールでよかったかも知れん…。