2月23日は富士山の日～。富士山って本当に綺麗ですよね！
…って、玄武岩の話しかしてねぇじゃん。
玄武岩といえばアア溶岩とかパホイホイ溶岩とか
アア溶岩というのはハワイの言葉で 玄武岩質なマグマがガサガサした感じに固まったものです。一方、水で練った泥を積み上げたように固まることもあって、そちらの形状はパホイホイと呼ばれます。
via Lava – Wikipedia (PD)
国際的に通じる火山用語がハワイの言葉ってのにグッと来ますが、アア溶岩の語源は「踏んだら痛くて思わず『ああっ』て言うから」ってことらしくて、なんだそれなんだそれすごすぎる。
在学中、火山学会の手伝いに投入されたことがあるんですけど壮年の先生方がパホイホイ パホイホイ連呼してるの見て和んだ覚えがあります。
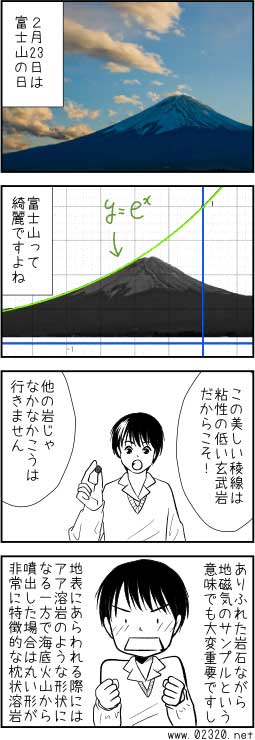
富士山と自然対数の底eにまつわる不思議な話
さて。
2コマ目の、富士山とネイピア数のグラフを重ねたものはサイエンスナビゲーター桜井進氏の図が有名です。
|
『桜井進 雪月花の数学』 |
ネイピア数 = e = 2.71828182… と呼ばれるこの数字、自然現象を扱おうとすると避けて通れない不思議な数ですね。
【 memo 】
自然対数の底と呼ばれることも。『1に「ある小さな数」を足して、その逆数回自身をかけ続ける』と得られる数字です。
nが大きくなるにつれて最初の数が1に近づくため、見た目の印象に比して大きな数字にはなりません。ただし、ゆるゆる増えていくわけでもなくて一定の数字に収束します。それが e 。
該当図を見たという人の「たまたま上手くはまるモチーフを選んだね」って意見を少なからず見かけるんですけど、噴出物が重力を得て広がっていくさまが物理法則と無縁であるはずもなく、それってまさに対数的概念なんだけど！って思います。
ちなみに粘性の高い安山岩質の山は お椀を伏せたような形になるので さながら「まんが日本昔話」に出てくる書き割りのような印象になります。
実際そういう地域は民俗学的にも昔話が良く残っていたりして、授業で各地の山を調査して回ってた頃は自然の形状が人の暮らしに与える影響を想像したりするのが好きでした。
【関連記事】
【一富士二鷹三茄子 vs 一姫・二太郎・三なすび】
富士山 x 数学で有名なもう一つのグラフ…のご紹介ですが、なんというか暦の話です。
|
|
雪月花の数学―日本の美と心に潜む正方形とルート2の秘密』【楽天】 / 【Amazon】
改めてご紹介。山の形が違っても摂理に忠実ならグラフと合致します。あと e の代表的な使用例は複利計算だったりするので「雪だるま式に借金が膨らむ」みたいな寓話はまさにこのグラフに従うのでありました。 |
コメントをどうぞ(´ω｀*)