東京オリンピックエンブレムの面積を求めて軸について回すのじゃ

本稿は、何かと話題の佐野研二郎氏デザイン東京オリンピック2020エンブレムを数学的にいじり倒す鯵坂もっちょ(@motcho_tw)さんのまとめ『東京オリンピックエンブレムの面積を求める』を全力で讃えるエントリーです。

あらすじ

例のエンブレムについて燃え上がっている真っ最中に突如として回ってきたまとめ『東京オリンピックエンブレムの面積を求める』。

記事を読みに行ったら冒頭のdescriptionが熱かった。

【数学】東京オリンピックエンブレムの面積を求める – Togetterまとめ
デザインが気に食わんとか、何かのパクリだとか知ったことではない。俺は面積が知りたいんだ。

まとめ pic.twitter.com/Qf8p9hBuI8

— 鯵坂もっちょ (@motcho_tw) 2015, 7月 29

こｗれｗはｗｗｗ

氏によると、エンブレムのうち色が付いてる面積は

【面積】
π(a/3)2 + 4a2/3 + 2(2a2/3 - 1/2arctan(4/3)(√10a/3)2)


となるようです。なるほど、金銀を抜いてる扇形は90度じゃないんですね。

話の流れとしては超好きなやつですが、arctanが出てきてるのに違和感あります。これもう少し綺麗にならないの？

自分でもエンブレムの面積を計算してみる

鯵坂もっちょさんが基準の長さにしたのは『外枠の正方形に内接する円の半径（＝大正方形の1/2辺）』でした。例えばこれを長方形の外接円の半径にしたらどうにかなりませんかね。

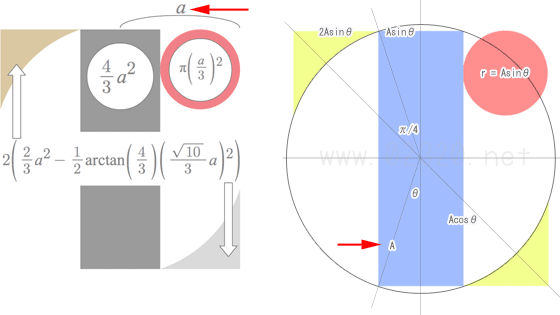
実際に計算してみたところ、開始2分くらいで方針転換を決めました。うわーヤッダこれ超面倒くさい！やめやめ！(ﾉ)ŎдŎ(ヽ)

…ということで、外接円の半径やめて長方形の1/2短辺を基準線にします。

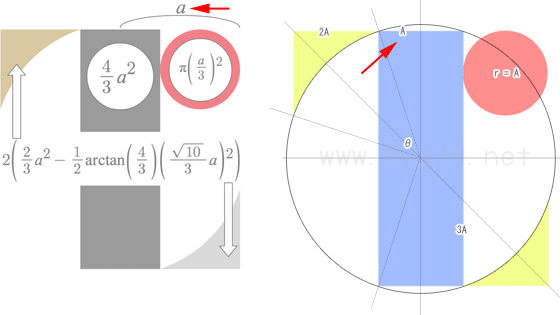
鯵坂もっちょさんが示す基準線の1/3の長さってことになりますね。（この時点で別解度が相当下がってるのは内緒だ。）

右上の赤い丸の面積

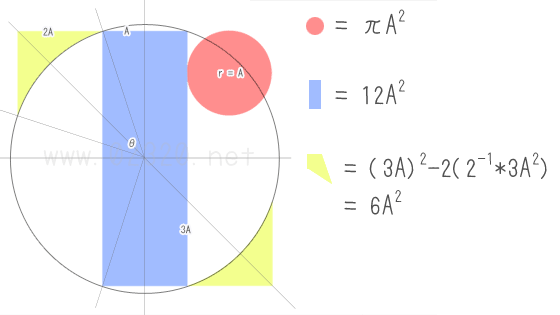
赤丸が大正方形と青い長方形に接してることから

【赤丸】
半径r = A
赤丸面積 = πA2


中央の帯の面積

外接円を単位円としたとき、(π/8-θ/2)の角を持ちAを高さとする青い三角形の底辺は3Aなので

【長方形】
長方形の面積 = 2A*6A = 12A2


大正方形と原点を結ぶ凧（ダイヤ）型の面積

1/4外接円で切り取られた1/4帯の斜辺は √10A 、
凧の短い対角線は直角二等辺三角形の斜辺より 2√2A 。

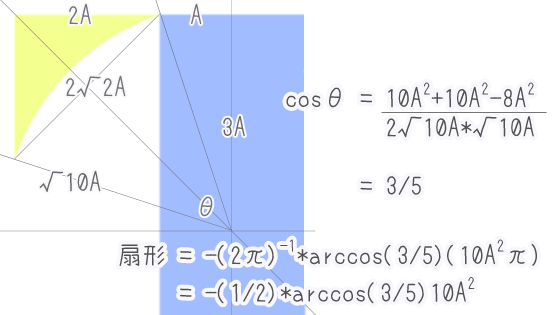
ここで、原点を含み上記の辺を持つ二等辺三角形について　余弦定理を用いると

【cosθ】
= ( 10A2 + 10A2 - 8A2 ) / ( 2√10A * √10A )
= 3/5


θ = arccos(3/5) が得られたので、凧の着色部の面積は

【凧の着色部】
= 6A2 - 1/2π arccos(3/5)(10A2π）


これが左上と右下で2個あるので

【凧の着色部2個】
= 2 ( 6A2 - 1/2arccos(3/5)*10A2 )


求める面積

【おち版】
求める面積
= πA2 // 赤丸
+ 12A2 // 長方形
+ 2 ( 6A2 - 1/2arccos(3/5)*10A2 ) // 凧の着色部


冒頭の鰺坂もっちょさんの結果が以下の通り。

【鰺坂もっちょさん版】
求める面積
= π(a/3)2 // 赤丸
+ 4a2/3 // 長方形
+ 2 ( 2a2/3 - 1/2arctan(4/3)(√10a/3)2 ) // 凧の着色部


ここで A = a/3 なので、

【鰺坂もっちょさん版’】
求める面積
= πA2 // 赤丸
+ 12A2 // 長方形
+ 2 ( 6A2 - 1/2arctan(4/3)*10A2 ) // 凧の着色部


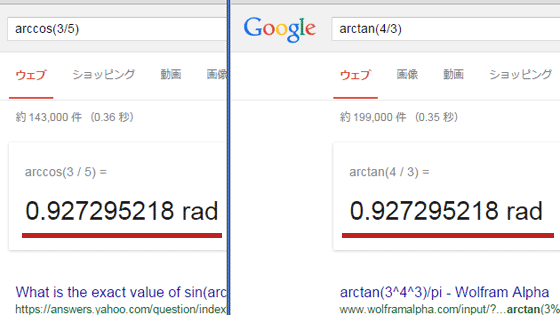
両者の違いは

arccos(3/5)
arctan(4/3)

のみです。ただし逆三角関数の定義により、言及している角はどちらも同じだとすぐに判るのがミソ。よって式の等価が示されました。

やっべ、難癖つけた割に大して変わらなかったでござる。(´・ω・`)

問2　積分せよ？

そんな折、はてブでコメント見てたら id:kubohashi さんのすごいの来ました。

あっこれ次はどっかの軸でくるっと回してできた立体の体積を求めるやつだ。

id:kubohashi のコメント / はてなブックマーク

出た－！問2！:;(∩´﹏`∩);:

回してみた

せっかくなのでモデリングして回してみました。

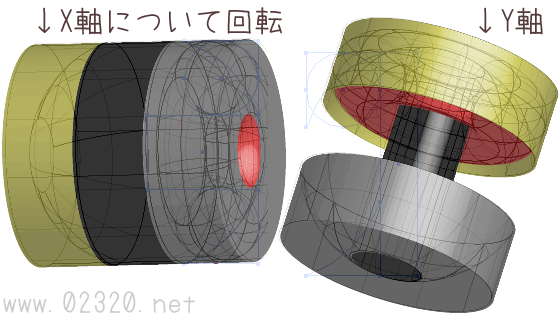
回しただけです。いつもより余計に回しております。丸いところ内側に変な隙間あるからね！

数学クラスタの皆さま、宜しくお納め下さいませ。

地学徒からは以上です！(; ・`д・´)