「数学って何の役に立つの？」に真っ正面から答えない論理学10題

「数学っていったい何の役に立つの？」という問いに対して、納得して貰える答えを提示することは非常に難しいです。

よく「図形の面積くらい求められないと困るだろう」などと回答する人がいますが、これは「算数」の領域であって質問者の意図を汲むものではありません。

命題それ自体の真偽に触れず数学の有用性を説くならば、対偶証明法あるいは背理法のような間接証明法を用いるのが良いでしょう。

対偶とは

対偶とは「ある前提（命題）」を等価に言い換えた概念です。命題「PならばQ」とその対偶「QでないならPでない」は構造的に命題と同じ領域を示しています。

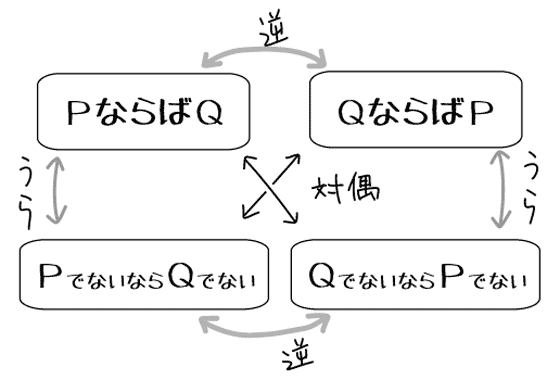
「PならばQ」が成り立つとき「QでないならPでない」は必ず成り立って、「PならばQ」が成り立たなければ「QでないならPでない」は必ず成り立たない。常に表裏一体の関係です。

基本	人間は	哺乳類だ	真
逆	哺乳類ならば	人間だ	偽（他にもいるから）
裏	人間じゃなければ	哺乳類じゃない	偽（例えば犬は哺乳類）
対偶	哺乳類じゃなければ	人間じゃない	真（ま、そうだろね）

人生の悩みを論理的に考える

命題と対偶は同じものだと言うことを踏まえた上で、誰もが知る格言について真偽を評価していこうと思います。

お客様は神様です

真偽判定に対偶を取る、最もメジャーな構文の一つです。「お客様は神様です」の対偶

「神でなければ客ではない」

は、明らかに例外が存在するので不成立。従って「命題自体が偽」となります。

ただし「神が素性を隠して地上で生活している可能性」もゼロではないので、神である客の存在も否定しません。偽だからと言って100％嘘じゃないことに注意。

聖☆おにいさん　中村光

神のような客でない限り、必ずしも客として扱う必要はない。

このように、自明と言いがたい命題の真偽を確かめるときに対偶を取ることは非常に有効です。モヤモヤした気持ちを論理学に託して先に進みましょう。

地獄の沙汰も金次第

何となく「金次第じゃないのは地獄の沙汰じゃない」と考えがちですが、体言化することで構造的な倒置が起きてます。

本質的には「金さえあれば地獄の沙汰もどうにかなる」と補える。「地獄の沙汰」とは「閻魔大王にどの地獄に送られるか」ということなので、対偶は

「楽が出来ないのは金がないから」

となりますね。

これはある種の真理です。つらい。

天高く馬肥ゆる秋

同様に対偶

「デブじゃないならまだ秋じゃない」

夏バテ、回復すると良いですね。

早く元気になれ～。∩(´・ω・`)つ―*’“*:.｡. .｡.:*・゜ﾟ・*

※本講には追記事項があります

お暇なら来てよネ

「来ないでネ　忙しい時は」

女のひとの怖み。

あの日あの時あの場所で君に会えなかったら

命題「あの日 あの時 あの場所で 君に会えなかったら僕等は いつまでも 見知らぬ二人のまま」

「僕らが知り合ったのは あの日 あの時 あの場所で出会ったから」

はい。

まとめ買いするなら今！

「今じゃなければまとめ買いしなくていい」

対偶が真に見えるという、まさかの「命題は真」の可能性について。

再帰的に、まとめ買いは「今この瞬間に特別な需要が存在する場合」のみ有効といえるでしょう。

あなたならどうする

「どうもしないのはあなたじゃない」

この理屈に乗っかっていくの割と男らしい気がする。

幸せなら手を叩こう

「手を叩かないなら幸せではない」

この命題の真偽判定は意外と困難です。文字通り取れば「手を叩いてない状態がすなわち不幸」なのはおかしいのですが、「手を叩く気分になれない人が幸せでない」ことに疑いの余地はありません。

命題「幸せなら態度で示そうよ」の対偶「態度で示さないのなら幸せじゃない」の圧倒的存在感と言えるでしょう。

つらい。

あきらめたらそこで試合終了ですよ…？

「試合が終了してないなら諦めてはいけない」

名作の対偶を取るの禁止。

ああ言えばこう言う

「こう言わなければああ言わない」

面倒臭い奴は無視しましょう。

補講：天高く馬肥ゆる秋

【 2015/06/18 追記 】id:SWIMATH2氏よりコメント頂きました。

「天高く馬肥ゆる秋」は連言なんだから、この命題の待遇ならド・モルガンの定理より「秋でないならば天が高くないまたは馬が肥えてない」だし、そもそも「～ならば秋」じゃなくて「秋ならば～」の形なのでは？
id:SWIMATH2 さんのコメント

仰る通りです。「空が高い＝上空に巻雲が多い（⇒秋）」というところから雑に開きすぎました。真面目にやります。

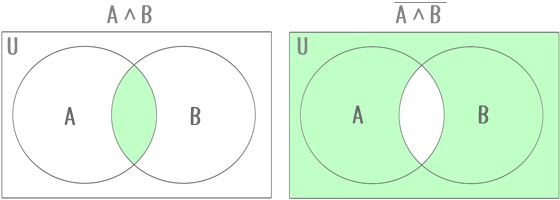
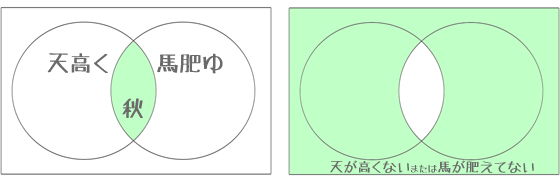
前半、ご指摘の通り「天高く馬肥ゆる」の補集合はド・モルガンの法則により「天が高くないまたは馬が肥えてない」となります。

もともと本故事は杜審言（としんげん）の詩『蘇味道に贈る』の「雲浄くして妖星落ち、秋高くして塞馬肥ゆ(雲淨妖星落，秋深塞馬肥)」に拠るもの。これをそのまま解釈すると「空が高くなり秋も深まれば馬も肥える」となるので、確かに「秋ならば～」の方が適切かも知れません。

一方「なぜ季節の移り変わりに気を留めているのか」というと、秋は「北方の騎馬民族が略奪に来る季節」であるのがその理由です。「襲撃に備えて警戒しなければならない、それが秋だ」という緊張感が「天高く馬肥ゆる秋」に集約されているのだと理解しています。

なれば詩から独立して成句になった時点で述語は『秋』一択、「天高く」はある種のきっかけでしかなく「秋を直接連想するのは馬体の充実」だろうという解釈でした。

…とは言えあくまで解釈のひとつであり、前提抜きに扱ったことは私の落ち度です。申し訳ありません。＞＜

人生に役立つ数学入門

高校時代は「間接証明考えた奴ふざけんじゃねぇよ！バーカバーカ！」って心の底から思ってましたが、ピンポイントにはまると大変エレガントな手法だと思います。使いどころを間違えると詭弁になっちゃうんですけど、客観的に眺めるためのツールとして有用。

数学が人生で何の役に立つのかと言う意味で、三角関数や微積と縁遠い一生を送る人は実際それなりにいるのでしょう。でもだとしても、数理論理学くらいは真面目に受けとくと良いのでしょうね。集合論とか文系でも普通に使いますし。

極論を言えば数学と呼ばれる領域は「算数と物理と哲学」に分けられて、物理計算以外の部分はみんなやっといて損はないと思います。